Counterexample-Guided Directed Fuzzing via Likely Invariant Inference

  • 引用：Huang H, Zhou A, Payer M, et al. Everything is Good for Something: Counterexample-Guided Directed Fuzzing via Likely Invariant Inference[C], 2024 IEEE Symposium on Security and Privacy (SP). IEEE Computer Society, 2024: 142-142.
  • CCF A S&P , IEEE Symposium on Security and Privacy
  • 链接

1 摘要

  • 定向模糊有很多应用，如 补丁回归测试[1,2],漏洞重现[3,4],验证静态分析报告[5,6],为各种漏洞生成概念验证输入[7]
  • 现有定向模糊测试输入许多都与目标无关，我们称为indirect input generation。
    • [10,12-16] 使用种子突变，产生95%的输入与目标无关
    • [17,18,19] 拒绝了一些输入，但仍然有大量无关输入
  • 本文提出一种高效的，定向灰盒fuzzing技术来解决indirect input generation。
    • 关键见解是通从可达和不可达的执行输入中推断出可能的不变量，以限制后续输入生成的搜索空间并产生更多可达的输入。
    • 此外，为了高效的产生输入满足目标状态，我们提出两种策略优化可能的不变量推理，
      • distance-based input selection，减少输入使得不变量推断更加高效
      • similarity-based invariant selection，消除不准确的不变量使得输入生成更加高效
  • 我们在灰盒fuzzer Halo实现了我们这个输入限制的模糊测试方法
    • 使用Magma[20]benchmark
    • 4种SOTA directed fuzzers:AFLGO[10],Beacon[17],WindRanger[15],SelectFuzz[16]
    • 4种SOTA non-directed fuzzers:AFL[21],AFL++[22],ParmeSan[23],SymCC[24]
    • 结果现实，Halo6.2x产生可达输入，漏洞重现快15.3x,并检查出了更多的漏洞
  • 本文贡献总结
      1. 提出利用已执行的输入动态推断可能的不变量，以限制后续输入生成的搜索空间，从而加速定向模糊测试中的漏洞重现过程
      1. 设计了两种新颖的选择策略，以提高输入生成的效率，有效地减少了生成的不相关输入的比例
      1. 我们提供了实证证据证明我们的方法比SOTA定向模糊器更高效，有效

2 动机

  • 2.1：现有工作的intuition及 justify 他们的弱点
  • 2.2：陈述我们解决这些问题的动机

2.1 Existing Directed Fuzzers

  • 定向模糊测试的主要目的：examine the program behaviors defined by the targets.
  • 现在SOTA定向模糊测试中，主要有两种趋势
      1. 通过选择promising seeds来接近目标
      1. 消除无法达到目标的输入的不可达执行
2.1.1 Sophisticated Seed Scheduling
  • [10,12,13,14]致力于选择具有最高检测目标行为概率的种子,使用各种使用度函数衡量达到目标的可能性
    • AFLGO[10] 优先考虑与控制流图中目标的最小距离的种子
    • Hawkeye[13] 通过考虑从崩溃报告中获得的平均“call-trace-distance”来优化此距离度量
    • CAFL[12] 通过必要的指令来细化调用跟踪以触发崩溃
    • WindRanger[15] 通过仅收集从控制流偏移块到目标的距离来改进适应度
    • SelectFuzz[16] 通过数据依赖仅计算从变量和块到目标的距离。另一种方法是衡量达到目标的困难程度
    • MC2[14] 将定向模糊测试转换为蒙特卡罗计数模型，使用每个分支的执行频率来近似达到目标的困难程度，并优先考虑具有最低困难度的种子。
  • 尽管有许多基于优先级的方法帮助fuzzing更快地定位到目标，但主要的输入生成方法依赖随机突变，只有一小部分有限的种子输入，结果导致大量的无关输入被运行
2.1.2 Culling Infeasible Executions
  • 一些fuzzer-created inputs绝不会达到目标行为，为了减少这些运行，一些fuzzer会在清除知道不会达到目标的时候停止执行[17,18,19]
    • FuzzGuard[18] 使用机器学习模型预测是否可达
    • Beacon[17] 推断必要的达到目标的preconditions，如违反则停止执行
    • SieveFuzz[19] 提出根据动态反馈自适应地优化可以被除去的路径，减少不可达的执行
  • 尽管拒绝一些输入可以提高效率，但这仍然是一种补偿性措施，因为没有迹象表明可以直接生成针对目标的输入。

2.2 Example and Key Challenges

  • 图1中，假设我们有三个种子
    • A(a,b,c,d):(15,5,10,10)A(a,b,c,d):(15,5,10,10)
    • B(a,b,c,d):(5,5,10,10)B(a,b,c,d):(5,5,10,10)
    • C(a,b,c,d):(15,5,10,0)C(a,b,c,d):(15,5,10,0)
  • 现有fuzzer可以优先选择种子 B 而不是种子 A 和 C，因为种子 B 可以到达第 12 行，而种子 A 和 C 到达第 11 行，但是随机变异种子可能不会快速满足第 11-13 行的紧密路径条件，更不用说满足溢出条件 a + b + c > sizeof(buf)
  • 虽然种子 B 被优先考虑，但是模糊测试工具仍然可能生成大量违反路径条件的输入，导致探索与目标无关的程序，例如第 18 行的代码块。
  • 另一方面，消除导致目标的不可行执行并不帮助生成朝向目标的输入。例如，Beacon [17] 可能根据可达性和路径条件终止执行。因此，一旦执行到达第 18 行，模糊测试工具可以停止执行输入。然而，模糊测试工具仍然缺乏如何生成满足第 11-14 行条件的输入的知识
Motivation
  • 存在 indirect input generation 的问题的关键原因是输入生成对目标路径条件的无视。我们注意到，即使现有方法可以通过额外的反馈优化种子选择或消除不必要的执行，我们仍必须为 定向模糊测试 特化输入生成，以便更快地到达目标。
  • 然而，到目前为止，现有方法错过了这个优化机会，具体来说，现有方法仅保留了执行种子时的少量反馈哦，仅占生成输出的一小部分，大多数输入在执行后被丢弃
  • 例如，下表显示，SOTA AFLGO在Magma基准测试中仅保留了少于0.01%的执行输入反馈，因此在我们4.1AFLGo 不能有效地重现大多数目标（基准测试中的 138 个目标中的 19 个）
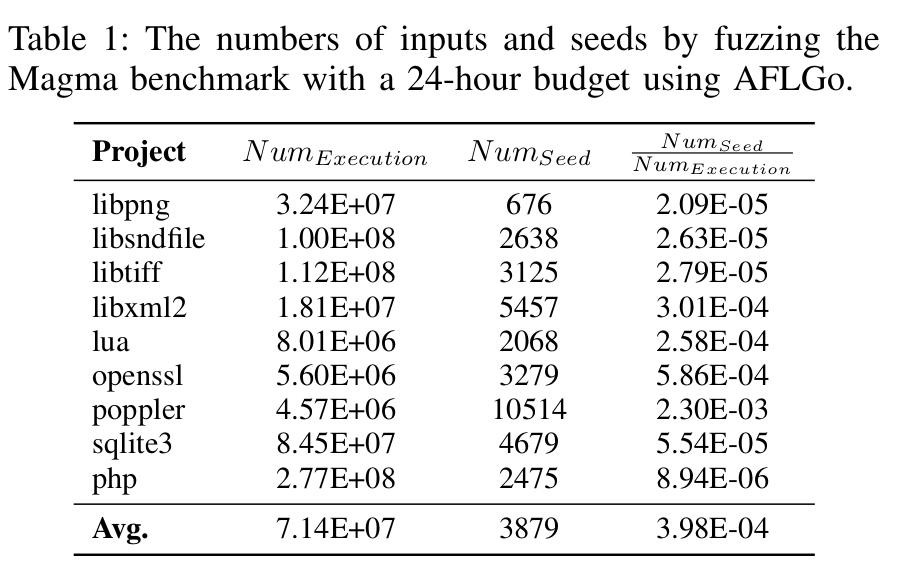
  • 因此，我们的想法是利用执行的输入来近似目标条件，这可以限制后续输入生成的搜索空间。
  • 我们使用图2说明我们的基本想法。输入可以视为从各种程序路径的分布中取样，这些路径的条件（谓语）是区分路径的边界。由于fuzz高效的输入生成速度，我们可以通过大量样本推断这些边界。
    • 例如，通过观察上一个例子中对种子A，B，C中的a值进行变异生成的输入，我们可以近似认为达到目标的条件是a<15,其是11行的否定条件的一个值，尽管还没有达到a<10，但之后就不需要生成a>=15的输入。此外，如果发现反例a=10，则可以进一步改进这个近似
  • 目前，有效地近似条件和生成输入面临两个主要挑战：
  • Challenge 1. How to infer conditions from executed inputs efficiently?
    • 为了实现高效性，模糊测试工具必须以尽可能少的输入准确推断条件。
      虽然模糊测试工具能够生成大量输入，但为每个输入记录反馈可能会带来显着的开销。
      因此，需要有效的输入选择策略，仅选择必要的输入进行条件推断，从而最大程度地减轻对模糊测试工具资源的负担。
  • Challenge 2. How to generate inputs constrained by conditions efficiently?
    • 为了有效地重现目标，模糊测试工具应该使用推断的条件高效地生成受限制的输入，而不是持续调用昂贵的约束求解器。
    • 然而，条件可能各不相同，而并非所有条件都同样有用；例如，条件 b > 1 与条件 a < 10 分别相比对变量 b,a 的搜索空间的约束可能不那么显著。
    • 条件复杂化不仅可能减慢输入生成速度，还可能导致生成的输入未能达到目标。
    • 因此，有效地确定推断条件的有用性对于提高输入生成的质量至关重要。

3 Counterexample-guided Directed Fuzzing

  • 接下来介绍Halo，一个定向fuzzer可以有效的通过使用条件估计限制输入来生成导向目标的输入
  • 如图3示，我们的核心功能是基于fuzzers生成的输入的运行来推断出一系列可以代表环境路径的不变量（Section3.1）. 为了有效地推断不变量（Chanllenge 1），我们通过选择具有代表性的可以准确推断不变量的输入，减少了推断引擎的输入数量（Section3.2）.为了更好地生成满足不变量地输出（Challenge 2），我们根据来自模糊测试的自适应执行反馈来降低那些不能精确描述路径条件的不变式的优先级，这样做是为了增加生成可行输入的概率

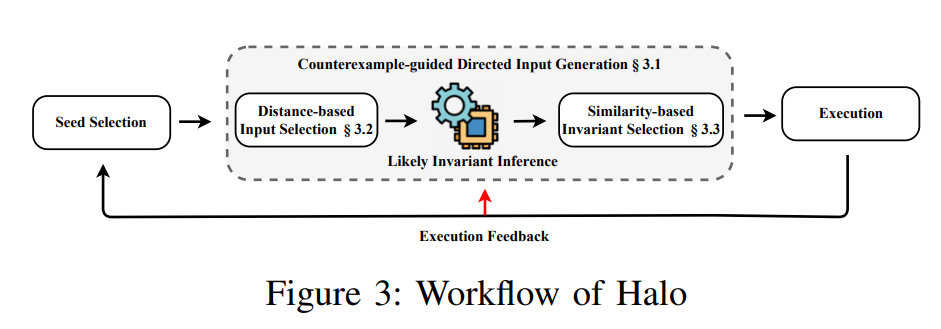
3.1 intuition: Approximating the Condition with Dynamic Likely-Invariant Inference

  • 算法如下图示
    • 当fuzzer开始根据所选种子生成输入时，line 2
    • Halo通过基于一系列通过种子生成的输入估计导向目标的条件 line3-8
  • 直觉上，路径条件可以被视为一个满足多个输入的不变量，因此，我们的基本直觉是找到可以满足所有输入的不变量作为目标条件的估计。
  • 根据这个直觉，我们提出了一种轻量级方法，灵感来自[25],不变量作为输入表示的目标路径条件的近似值，可以约束后续输入产生
Algorithm 1 Counterexample-guided Directed Fuzzing
Require: Seeds S, Target t
1: repeat
2:      s, I_use ← ChooseNext(S) //I_use为使用的不变量
3:      if I_use = ∅ or I_use is not effective then
4:          Sreach, Sunreach ← InputSelect(s, t) (§3.2)
5:          Ireach ← InvInfer(Sreach)
6:          Iunreach ← InvInfer(Sunreach)
7:          I_use ← InvSelect(Ireach, ¬Iunreach) (§3.3)
8:      end if
9:      Inputnew ← Sample(I_use)
10:     Tracing(Inputnew)
11:     Havoc&Splice(s)
12: until Timeout is reached
Preliminary of Invariant Inference
  • 使用一系列输入 SS ，推断引擎推断出一组不变量 II ，对于 ∀x∈S,x∣=i,(i∈I)\forall x \in S , x |= i,(i\in I) ，我们使用I来近似 达到目标所需的条件路径
  • 现有的不变量推理方法[25,26,27]通过分治搜索来获得精确的肯呢个不变量，并保证算法的种植。具体来说，不变量推理从形式范围 [min,max][min,max] 的过近似开始，对于一组不变量模板，c1t1+c2t2...+cntn≥0c_1t_1+c_2t_2...+c_nt_n\geq 0,其中包含n的系数c，和关系t，由程序变量的多项式组成，用于近似路径条件
  • 根据给定输入，推理引擎首先检查输入时候能够在执行时满足当前不变量，如果可以不发生任何变化。否则，算法会根据反例来缩小输入范围，同时，没有有效范围的模板不变量将被丢弃
  • 因此，不变量推理的准确度取决于给定的输入和模板不变量。随着更多输入的提供，算法逐渐细化不变量得到更高的精度
  • Example 3.1
    • 假设推断引引擎从 $(-\infty,+\infty) $ 推断三个模板不变量 a,b,a+b,来估计图1中12行的状态
    • 对于给定输入 a=5,b=0a=5,b=0 , 推断引擎通过运行反馈发现其不能满足条，随后缩小不变量的范围 a∈(5,+∞),b∈(0,+∞),a+b∈(5,+∞)a\in(5,+\infty),b\in(0,+\infty),a+b\in(5,+\infty) 来提高精确度
  • 本工作的目标不是改进不变量推理算法，而是明确地应用不变量推理改善定向模糊测试
    • 具体来首，我们使用SOTA不变量推理引擎Dig[26]. 采用的模板不变式包括常数检查、涉及单个变量的下界检查以及多个变量之间的线性不等式依赖关系(这些在现有不变量推理技术中广泛被作为默认设置[25,26,28,29])
  • 值得注意的，选择理想的不变量模板仍是动态不变量推理的一个挑战，这不是我们的值嗯点，我们将在第5节提供更多工作细节
Input Collection
  • 通过fuzzing生成的大量测试用例，Halo可以推断不变量来促进更好的输入生成。
  • 具体的，Halo记录input和他们到达目标的值（算法1中line 4）
  • 我们使用执行反馈将输入分为两组：可达和不可达的输入，以便推断不变量。Section3.2描述了分组的相关细节
  • Example 3.2
    • 考虑图一中的程序有五个输入没有触发崩溃
      • A(a,b,c,d):(15,5,10,10)A(a,b,c,d):(15,5,10,10)
      • B(a,b,c,d):(6,8,10,10)B(a,b,c,d):(6,8,10,10)
      • C(a,b,c,d):(12,5,30,0)C(a,b,c,d):(12,5,30,0)
      • D(a,b,c,d):(6,10,12,0)D(a,b,c,d):(6,10,12,0)
      • E(a,b,c,d):(6,100,12,0)E(a,b,c,d):(6,100,12,0)
    • Halo记录输入字节影响变量abc的及他们的值
      • Sreach=B:(6,8,10),D:(6,10,12),E:(6,100,12)S_{reach} = B:(6,8,10),D:(6,10,12),E:(6,100,12)
      • Sunreach=A:(15,5,10),C:(12,5,30)S_{unreach} = A:(15,5,10),C:(12,5,30)
Invariant Inference

  • 通过分组的不变量，我们推断不变量 Ireach,IunreachI_{reach},I_{unreach} 为每个组的输入 （算法1 Line5-6）

  • Ireach,IunreachI_{reach},I_{unreach} 分别表示达到目标的可能条件和没有触发目标的条件，因此，我们新生成的不变量需要满足 IreachI_{reach} 并且满足 IunreachI_{unreach} 的反面

  • Example 3.3

    • Ireach=a<7,b>7,c≤10I_{reach} = a<7,b>7,c\leq 10
    • Iunreach=a>12,b<6,c≥20I_{unreach}=a>12,b<6,c\geq 20
    • 此时我们可以确定输入满足
      a<7,a≤12,b>7,b≥7,c≤10,c≤20a < 7, a ≤ 12, b > 7, b ≥ 7, c ≤ 10, c ≤ 20
Remark 1 讨论1
  • 与传统的通过符号执行推断精确的推断路径条件相比，推断不变量是一种轻量级的估计，尽管比实际路径条件要不准确一些
  • 然而，通过可达不变量和不可达不变量，也足够用来高效的筛选不可达输入生成
  • 仅利用执行反馈和输入，在处理复杂程序行为时（如循环）具有更好的延展性。
  • 此外，与现有动态不变量推理方法不同，后者由于记录执行过程中的中间值而引入了显著的运行时开销，导致了可扩展性问题[26],我们只推断输入之间的关系以解决indirect input generation问题，从而减少了开销
  • 尽管筛选推断出不变量过滤unreach输入是有效的，但在处理大的输入搜索空间且伴随 （1）爆炸性输入 （2）复杂关系时，使用不变量推理进行模糊测试仍十分困难
  • 因此，我们的目标是最小化这两个因素在不变量推理中引起的维度爆炸，以提高模糊测试的可扩展性

3.2 Efficient Invariant Inference with Distance-based Input Selection

  • 尽管提升输入的数量可以提高不变量推理的准确性，但是这会导致不变量推理引擎的运行时间增加，同时会导致缺陷提升，因为生成的输入可能不会满足目标条件
  • 为了高效的推断准确的不变量，我们的目标时使用最小化的代表性输入来准确的描绘目标条件。具体的，我们观察到每个输入对准确推断不变量的贡献不同，这将激励我们最小化不变量推断需要的输入集合
  • Example 3.4
    • 考虑 Example3.2中的输入，我们注意到输入 EE 没有改变推断结果因为其被 DD 包括了。因此我们不需要在推断中使用 EE ，这样可以减少不变量推理的开销
  • 然而，量化不变量推理中输入的有效性是一项具有挑战性的任务。为了解决这个问题，我们可以将输入分布视为数据聚类问题，只有接近条件边界的输入才能有助于推断不变量。原理边界的输入无法有效地描述目标条件。
    • 例如，图4中红线所示额的范围之外的输入比红线内的输入更不可能产生精确的不变量。因此，我们可以根据输入距离条件边界的距离来选择输入
How to Select Inputs

  • 基于前面的灵感，我们设计了一种基于距离的输入选择策略来选择可以有效推断不变量的输入

  • 距离维度描述了每个输入距离边界条件的接近程度

  • 如图2示，路径条件可以视为一个函数 f(x)f(x), xx 为相关输入向量。 f(x)=0f(x)=0 表示边界条件, ∣f(x)∣|f(x)| 为到边界的距离，因此，我们可以通过计算 ∣f(x)∣|f(x)| 来选择输入

  • 具体来说，在第一次突变种子之前，我们使用基于推理的污点分析 (inference-based taint analysis)[30-34]的过程，通过逐个字节地变异来获取影响到目标的输入。

  • We leave potential customization and fine-tuning of taint analysis as future work.

  • 在分析过程中，我们还记录了这些相关字节和 ∣f(x)∣|f(x)|

  • 为了方便计算，我们使用未出现在循环中的分支条件的值作为 f(x)f(x) 。因此，Halo可以保留一组接近目标且 f(x)f(x) 较小的输入集

  • Example 3.5

    • 假设在图1的程序中，我们有三个输入 B(a,b,c,d):(6,8,10,10)B(a,b,c,d):(6,8,10,10), B(a,b,c,d):(6,10,12,0)B(a,b,c,d):(6,10,12,0), C(a,b,c,d):(6,100,12,0)C(a,b,c,d):(6,100,12,0)，我们可以结算 f(x)f(x) 为，每个输入在 line 11-13 行条件判断的距离

      • ∣f(B)∣=20−12+14−10+20−10=22|f (B)| = 20 − 12 + 14 − 10 + 20 − 10 = 22
      • ∣f(D)∣=20−12+16−10+20−12=22|f (D)| = 20 − 12 + 16 − 10 + 20 − 12 = 22
      • ∣f(E)∣=20−12+106−10+20−12=112|f (E)| = 20 − 12 + 106 − 10 + 20 − 12 = 112
    • 因为 E 的距离里边界最元，我们只选择B和D作为代表性的输入在不变量推断中
  • 然而，对于没有达到目标的输入，我们无法获得距离，因为 f(x)f(x) 无法执行
    • 因此，Hao根据是否达到目标来分离用于不变量推理的输入
    • 在达到目标之前，Halo仅利用不可达的输入来推断所有输入字节的可能不变量，这表明可达输入不应该满足的条件
    • 通过否定从不可达输入推断出的不变量，fuzzer仍然可以限制生成输入的搜索空间
  • Example 3.6
    • 假设我们有不变量 Iunreach:{a>12,b<6,c≤20,d<10}I_{unreach}:\{a>12,b<6,c\leq20,d<10\},从Example3.2中不可达的输入中推断出
    • 尽管我们可能无法在 a∈10,11,12a∈{10,11,12} 时使用否定不变量过滤可达输入，因为 a≤12a≤12 从 II 中的 a>12a>12 不可达，而 a<7a<7 在 II 中可达，但模糊器仍然可以有效地过滤来自 a>12a>12 和 c>20c>20 的输入。
How many Inputs Selected
  • 我们基于计算需要的最小采样的统计理论决定选择多少输入来推断不变量[35]
  • n=4Z2ε2=385n = \frac{4Z^2}{ε^2}=385, 其中 ZZ 是 Z−scoreZ-score 决定错误 ε=0.05ε=0.05 的概率，即 95%95\% 的置信度
Remark 2
  • 不像现有定向模糊方法只通过种子存储临时变量，Halo通过从运行输入保留更多运行反馈来限制进一步的输入的搜索空间。
  • 基于这一直觉，输入选择旨在在数据收集的额外时间成本和推断不变量的准确度之间取得平衡。
  • 此外，利用从可达和不可达输入推断出不变量不仅提高了方法的可扩展性，而且从两个方向压缩近似搜索空间，有助于提高精确度

3.3. Effective Input Generation with Similarity-based Invariant Selection

  • 虽然可能的不变量可以帮助约束后续输入生成的搜索空间，但推理引擎可能会提供多个具有不同精度的潜在不变量，这可能不能平等地过滤掉不可达的输入。

  • 根据给定的输入，不变量可能会被过度约束。例如，仅从早期不可达输入推断出的不变量。

  • 因此，使用所有不变量进行输入生成可能会引入显着的开销，而没有提供足够的精度。

  • Example 3.7

    • Example 3.3中推断的不变量
    • 与不变量 c<10c < 10 相比，c≤20c ≤ 20 可以更精确地描述在第13行的路径条件 c<20c < 20
    • 不变量 a<7a < 7 过度约束，因为可达的 a∈7,8,9a ∈ {7, 8, 9} 被过滤掉了。

  • 为了有效地生成受不变量约束的输入，我们的基本直觉是根据新的输入生成 adaptively 地选择和细化不变量。

  • 如图5所示，理想情况下，由最精确的不变量生成的输入应始终满足路径条件。精度损失由在近似分布中找到的反例表示。更精确的不变量应生成更少的反例。

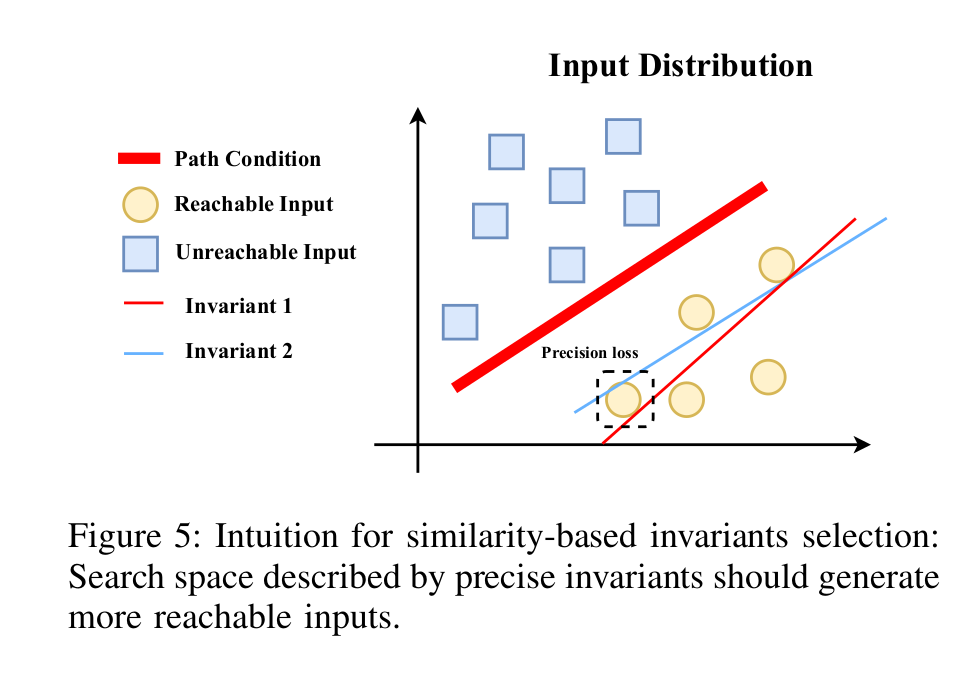
  • 因此，我们利用生成的输入的执行反馈来估计哪个不变量更类似于原始路径条件。

  • 相似性可以视为使用推断的不变量生成更多可达输入的概率。Halo根据在后续输入生成中发现的反例比率对推断的不变量进行优先选择。

  • 因此，由选定不变量描述的相似搜索空间可以提高生成可达输入的效果。

How to Select Invariants

  • 我们设计了一种基于相似度的不变量选择方法来自适应地选择生成可达输入最有效的不变量

  • 每个不变量的相似度被用于fuzzer选择该不变量的概率，相似度越高越容易被选中。

  • 我们用不变量生成可达输入的占比 Φ\Phi 来衡量相似度

    Similarity(Φ)=nNSimilarity(\Phi)=\frac{n}{N}
    其中 nn和NN是生成的可达输入和总输入的数量

  • Example 3.8

    • 假设我们使用从 Example 3.3中获得的不变量生成输入。Halo可以迅速找到条件 b≥7b\geq 7,单这是对 bb的过度限制，因为根据图1Line12，其值与 aa 的值也有关系。
    • 因此，Halo通过反例降低了该不变量的优先级，来避免生成不可达输入的反例
Input Generation with Adaptive Invariants
  • 直观地说，由于我们推断的不变量是线性的，它们可以形成一个多面体，描述了可达输入的搜索空间。
  • 因此，我们使用了SOTA采样技术，Vaidya walk[36]，它可以在线性复杂度的基础上从在大量不变量组成的多面体中高效地采样生成输入。
  • 此外，不变量的相似度基于后续的fuzzer输入生成不断地在更新.如果所有推断出的不变量都无法有效地生成优先级较高的可达输入，Halo会收集发现的反例，并推断出一组更具精度的新不变量，以保持输入生成的有效性。
Renmark 3
  • 我们从搜索空间的角度来解决有向模糊测试中的输入生成问题，这使我们能够在不解决精确路径条件的情况下有效地对可达输入进行抽样。
  • 同时，这种想法激励我们通过利用执行的输入作为回归来完善不精确的搜索空间
  • 于不变量是实际路径条件的近似，精度的潜在损失可能会不准确地扩大或缩小近似的搜索空间，从而阻碍其在生成可达输入方面的有效性。
  • 此外，与使用现有的不变量推断中的动态程序分析可能导致的潜在运行时开销相比[26]，[28]，[37]，[38]，我们利用模糊测试中可用的大量输入，这些输入近似于搜索空间的分布，作为选择精确不变量的轻量级预测器。因此，在模糊测试过程中，我们可以减少选择的不精确或多余的不变量的数量，从而更有效地生成可达输入

4 评估

5 Discussion

5.1 Potentials

  • Assisting Dynamic Analysis with Fuzzing
    • 动态分析已得广泛应用
      • 污点分析[43,44]
      • 程序合成[45,46]
      • 特征生成[47,48]
    • 与传统的静态分析相比，动态分析可以通过执行反馈提供更精确的结果。
    • 然而，对于动态分析，在没有足够数量的输入的情况下彻底分析程序具有挑战性[49]
    • Halo使用最先进的fuzzer生成足够的输入，以便动态分析来近似程序语义。此外，我们的输入选择策略可以有效地控制输入数量，实现更好的扩展性。
    • 除了Halo中通过可能的不变量近似的路径条件来处理内存安全问题外，还可以考虑复杂语义，如状态机模型和部分顺序约束，以支持检测涉及逻辑正确性的漏洞。
  • Semantic Extraction from Inputs
    • 虽然模糊测试的主要趋势之一是以不同的粒度提取目标程序的语义，例如使用符号执行来解决路径条件，但Halo中由执行输入推断的不变量指示了模糊测试的另一个潜在方向：利用观察到的不可达执行来防止模糊测试器不断探索无关的程序行为。
    • 在Halo中，我们还根据不可达输入推断不变量，以约束后续输入生成的搜索空间，从而有效地接近目标漏洞。由于模糊测试器可以生成大量的输入来检查程序，因此除了覆盖范围之外，还可以从执行的输入中提取更多的语义，以引导模糊测试器探索程序。

5.2 Limitations

  • Scalability of the Invariant Inference
    • 虽然动态的可能不变量推断优于符号执行，但其有效性仍可能受到可扩展性问题的影响，例如由于给定输入的过大或候选不变量过多
    • 为了环节这些问题，Halo选择适当的输入样本进行推断，并声称精确的不变量以生成输入，然而我们尚未优化候选不变量的质量，以提高近似目标条件的精度。因此，Halo的性能在尚未评估的其它项目可能受影响。然而该问题与定向fuzzing无关，参见6.2相关工作
  • Solving Complex Path Conditions
    • Halo的强大之处在于可以用可达和不可达输入中的不变量来约束搜索空间
    • 尽管我们在表4中展示了从不可达输入中推断处不变量的有效性，但与使用两类输入的不变量相比，其有效性较低。例如，达到目标的改进比例小于触发时间的改进比例
    • 为此，可以将Halo与其它输入生成技术结合，例如混合模糊测试与符号执行，以更快地达到目标并收集两个类别的输入。同时，基于AFL++的Halo实现也使得与基于AFL的模糊测试框架集成成为可能。
  • Support to Rich Semantics
    • 除了复杂的路径条件之外，漏洞可能涉及各种丰富的语义。例如，网络服务器中的逻辑错误可能需要程序执行满足特定协议的函数。
      然而，由于本文的主要重点是路径条件，Halo可能无法有效地复现这种类型的目标漏洞。尽管如此，我们仍然希望将这些问题总结为Halo解决的不同问题，并在今后的工作中讨论，如第5.1节所述。

6.1 Sophisticated Input Generation

  • Mutaing Relevant Bytes
    • 优化突变的一个主要趋势是突变相关的输入偏移以满足未覆盖的分支条件。
      • 除随机突变外，Fairfuzz [50]确定了不需要更改值的输入偏移，因此，最小化输入搜索空间提高了突变的效率。
      • ngora [51]采用字节级污点跟踪来发现目标条件的相关输入字节，然后应用基于梯度下降的搜索策略。
      • Redqueen [32]提出使用中间值作为反馈来修改输入中的值。
      • PATA [30]通过区分不同的路径和上下文来提高污点分析的精度。
      • Parmesan [23]利用从 santizers [39] 获取的标签来最小化需要被污点分析分析的分支数量。
    • 然而，这些方法都需要特定的分支来找到相关的字节。与基于覆盖引导的模糊测试不同，有向模糊测试无法选择分支，因为确定哪个分支可以更快地达到目标是具有挑战性的。有些分支甚至可能不满足目标的路径条件。因此，明确地为有向模糊测试调整这些方法是具有挑战性的，这也是为什么 Halo 只利用不变量推理来处理输入字节，而不是分析整个程序的原因。
  • Leveraging the Constraint Solver

6.2 Efficient Invariant Inference

  • 不变量推理已经成为程序验证[57,58,59,60],软件测试[38,61,62,63]和属性检查[25,26,28,29,37,64,65,66] 中一种具有潜力的技术。其对于确保软件系统的正确性十分有效，因为不变量可以作为程序与其行为的形式规范。
  • 不变量推理的主要目标是高效地推断适用于所有程序行为的精确不变量。
    • 传统的基于验证的方法旨在准确检测不变量。现有工作的大多数努力[29,57,58,59,60,63]，使用抽象解释和符号执行来静态地逼近程序行为的固定点作为属性。古纳在他们在理论上很准确，但由于符号执行分析故有的扩展性问题，他们的效率受到限制。因此，他们的方法通常设计于具有假设的特定应用场景
    • 动态不变量推理技术不追求对整个程序的精确假设，并根据给定的输入推断不变量。
      • 从Daion[25,64]开始，现有文献监视执行跟踪以验证一组候选不变量并具体化系数和项
      • DIDUCE[66]放宽了不变量的假设，因为违规可能导致异常程序行为，并优先处理具有置信度的违规行为以进行故障定位。
      • 由于推断得到的不变量的质量高度依赖于给定的输入和模板不变量，现有工作利用从执行中提取的更多程序语义来提高不变量的准确性。例如，
        • DySy [37] 利用共轭执行来推理潜在的模板不变量。
        • iDiscovery [28] 利用中间符号状态进行增量不变量推理以提高不变量的准确性。
        • MRI [38] 提出将推理过程建模为搜索问题，并使用基于挖掘的方法获得精确的不变量。
        • Dig [26] 依赖于来自反例的执行反馈来剪枝不变量的不可行范围，并逐渐提高精度。
  • Halo使用的不变量推理引擎使用了上述见解，以实现更好的效率。到目前未知，现有工作没有专注于优化给定输入的质量[28]，而这是影响不变量推理效果的关键因素之一。相反，Halo利用模糊测试工具作为输入生成器，以提高不变量的精度，从而最终增强fuzzer本身的输入生成能力

7 Conclusion

  • 我们提出了Halo，通过生成的输入推断出的动态不变量引导的自我优化定向模糊测试，以显著提高生成可触发目标漏洞的可达输入的效果。
  • 动态不变量有助于限制Halo后续输入的生成的搜索空间，实证结果展示了我们设计的方法带来了显著的改进
    • Halo 在重现目标漏洞方面的速度提升了 15.3 倍
      生成的可达输入增加了 6.2 倍。
      此外，Halo 还发现了十个先前未发现的漏洞，涉及到七个以前漏洞的不完整修复，以及 Magma 基准测试中评估项目的最新修补版本的 CVE。

8 个人总结

  • 提出一种SOTA定向方法，方法重点是通过 动态不变量方法 从 已有fuzzing生成的输入中推断出不变量，随后使用这些不变量来约束后续输入生成的搜索空间，从而提高生成可达输入的效果
  • 本文体现了不变量作为约束条件的使用，对于测试用例生成技术，不变量可以约束生成的空间